在QCM-D测量中，耗散因子D提供了与频率响应互补的信息，但是如何理解这些信息呢？ 在本文中，我们将更深入地研究芯片在各种负载下的振荡行为，并仔细研究耗散因子D所揭示的信息。
频率和质量之间的线性关系
当芯片表面负载有薄而刚性的薄膜时，振荡频率将降低，这是质量增加的标志。根据Sauerbrey关系式，此时的振荡频率（f）的降低与质量或厚度的增加呈线性关系：
其中常数C为材料特性，n为协频数，n = 1为基频。对于基频为5 MHz的石英晶体，常数C为17.7 ng/(cm2∙Hz)。
纯弹性薄膜vs粘弹性薄膜
薄而刚性的薄膜和石英芯片一样是纯弹性的。当引入粘性组分，表面会形成粘弹性膜或柔性膜，系统中就会产生能量损失。现在让我们来研究一下吸附在石英传感器上的柔性膜，如水合聚合物材料在水相中的振荡行为。 图1A-B是振荡频率f和能量耗散因子D随薄膜厚度变化的函数。对于非常薄的薄膜（几纳米），f和D的响应都很小，且呈线性变化，Sauerbrey方程(eq. 1)仍能很好地描述该系统。随着厚度的增加（图1 A-B），f和D的变化进入非线性状态，且耗散因子D响应变得更为显著。
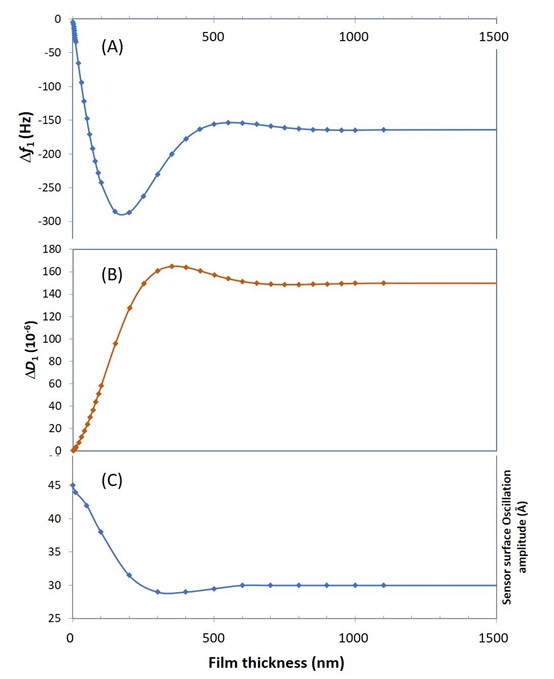
图1：在n = 1时，拟合的QCM-D响应随薄膜厚度变化的函数。频率f（图(A)）、耗散因子D（图(B)及传感器最大振幅（图(C)）随吸附层厚度的变化函数。
耗散因子D量化了振荡运动的衰减
当吸附层是刚性薄膜时，它会和传感器表面的振荡运动完美耦合。而当吸附层是柔性膜时，振荡所引起的粘弹性剪切波在薄膜中传播时会产生延迟运动。 剪切波的这种传播以及薄膜的柔性将对振荡运动产生阻尼作用，由此引起的能量损耗可通过耗散因子D对其进行量化。
声波的叠加会影响传感器的振幅
由于声波在薄膜-液面界面处的反射，在入射波和反射波之间可能存在正叠加或负叠加。图1C为传感器振荡幅度与薄膜厚度的关系图。
在与D的峰值重合处，传感器表面的振荡幅度从减小变为增大趋势。 由于声波的叠加，传感器表面所经历的运动阻力可以被放大或者减少。剪切阻力越小，振荡幅值越大，能量耗散系数越低。由于降低了所承受的质量负荷，负剪切阻力效应会同时减小共振频率。如图1A 中 f在150至500 nm之间的厚度，以及图1B中D在350至650 nm之间时厚度，就是由于上述声波叠加引起的变化。
需要注意的是，图1A中频率（f）的最小值与图1B中耗散（D）的最大斜率重合，而耗散因子（D）的最大值与频率（f）的最大向上斜率重合。 后者对应于在入射声波和反射声剪切波之间具有最大反相的情况，此时得到最大的能量损失，即得到最大的D值。而在前者对应的时点，则是质量最大，且能量损失的导数最大。
结束语
因此，很明显，f和D的形状会以不同的方式描述粘弹性情况。 如图2所示，当绘制Δf /ΔD的函数图时，可以更为清楚地看到，在某些情况下不可能仅从f得出正确的结论。 例如，ΔD为149∙10-6时，则它可以对应三个不同的Δf值-155，-161和-263 Hz。
图2.当n = 1时，以Δf对ΔD作图，拟合QCM-D的响应随薄膜厚度的变化函数。 图中所示，对于粘弹性薄膜，f：s和D：s可以是非唯一的。 例如，在该图中，ΔD= 149∙10-6对应于三个不同的Δf值-155，-161和-263 Hz。
可下载以下QCM-D中的耗散因子D能告诉我们什么信息？PDF版本，供以后使用。
参考文献：
24小时热线:400-833-6968
百欧林官方微信
