在与QCM技术相关的文章中,经常提到所谓的Sauerbrey方程。但是这个方程是什么,什么时候应该使用它?
Sauerbrey方程可用于计算薄膜层的质量
QCM技术能够测量质量变化是源于共振频率与质量之间关系的发现。1959年,当时在柏林攻读博士学位的Gunter Sauerbrey将它们之间的关系用一个方程式表示出来。该方程是振荡石英晶体的振荡频率与质量变化之间的线性关系,如式(1)所示。
Δm = − C ·Δf/n (1)
在实际应用中,这个方程可以用来计算增加到QCM晶体表面的薄层的质量。将薄膜质量增加引起的振荡频率变化∆f代入方程式1中,您可以得到薄层增加的质量∆m。常数C与石英的性质有关。对于5 MHz的晶体,C = 17.7 ng/(cm-2∙Hz)。参数n为奇数倍频数,可以是1、3、5、7……等。
什么时候可以使用Sauerbrey方程?
频率和质量的线性关系是基于纯石英晶体的行为,如下图1(左)所示,其中厚度为h(质量为m)的晶体具有一定的振荡频率。将一层不同于石英的材料添加到表面的情况可以近似于更厚的晶体,因此必须与“纯石英”情况非常相似。模型假设新的增加薄层可以近似于振荡晶体本身的一部分,现在厚度h +Δh(图1,右)。因此,传感器上的薄层必须是薄的、刚性的并牢固地附着在晶体表面上的,只有满足这些条件时才可以使用该方程。如果传感器上的吸附层是柔软、厚或未耦合到表面,这时这个方程是无效的。在这种情况下,模型会失效,计算出的质量会被低估。
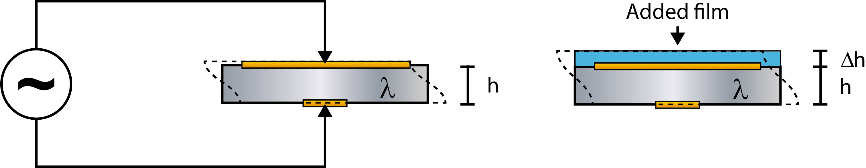
图1所示:石英晶体的原理图(左),厚度为h,质量为m,通过施加交流电压激发共振。具有附加质量的振荡晶体(右),此时厚度是h +Δh,质量是m +Δm。
怎么知道是否可以使用Sauerbrey等式?
如果您使用的QCM设备可以测量能量损失,或者能够在多个谐频下测量,则可以通过查看原始数据来确定Sauerbrey方程的适用性。原始数据将通过显示低能量损失或者重叠谐频(如果进行测量)来揭示适用性。如果Sauerbrey方程不适用,那么您需要使用一个更合适的模型来表征您的薄层特性,可能是粘弹性模型。
下载附件The Sauerbrey relation了解更详细讲解。