在耗散型石英晶体微天平（QCM-D）检测中，除了可以得到能量耗散因子D外，还可以通过监测多个倍频获取粘弹性样品的更多信息。 本文中，我们将针对具有各种不同厚度的理论聚合物薄膜，仔细研究其倍频所提供的信息。
每一个倍频为样品材料提供了不同的视角
根据物理定律，声剪切波δ在液体或柔性介质中的穿透深度将随着剪切振荡频率的增加而减小
其中η和ρ是介质的粘度和密度，ω是角频率。
作为Eq. 1的直接结果，不同的倍频会对传感器表面上的柔性薄膜层产生不同的响应。就像光学测量方法中不同的入射角度和波长一样，不同的倍频为样品材料提供了略有差异的视角。正如人们观察一个三维物体时（图1），为了从外观上获得完整的图像，需要从不同的角度观察它。 仅从一个角度进行观察将得到不完整的图像，甚至可能蒙蔽观察者，使其对物体产生误导性的描述。
图1. 从不同角度观察得到的三维物体示意图。
剪切振幅随谐频和传感器负载的变化而变化
如图2所示，压电谐振器的一个固有特性是传感器表面的振动幅度随倍频数的增加而减小。随着传感器负载的增加（本例中为薄膜厚度的增加），振幅的减小类似于Δf和ΔD相应的减小或增加。
当膜厚变化到一定值时，可以观察到最大的振荡振幅下降（图2）。这种情况发生时的厚度对应于所发射和反射的剪切波之间的最大反相位，随倍频数的变化而变化。
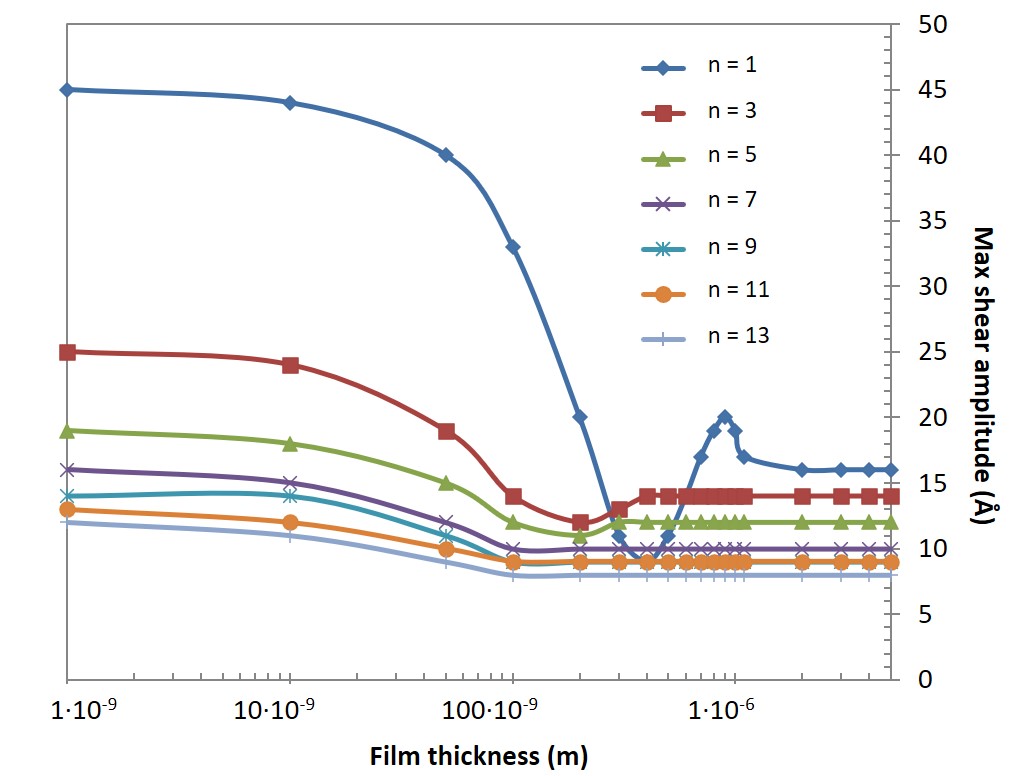
图2. 倍频为n = 1、3、5、7、9、11和13时，传感器表面最大剪切振荡振幅拟合值随膜厚变化的函数。图中显示，传感器表面的最大振荡幅值随倍频数的增加而减小。同时也可以看到，在一定的膜厚时，振幅会下降到一个最小值，该极值对应于发射和反射剪切波之间的最大反相位。
这种现象也可以在不同膜厚下整个膜的剪切波振荡振幅中清晰观测到（图3）。
1 nm厚的薄膜基本上是刚性的，并且比穿透深度δ薄得多。因此，整个薄膜的位移将基本保持恒定。
10 nm薄膜行为非常类似，不同之处在于，由于增加了质量负载，振幅变小了（图3A-B）。
当薄膜厚度增加到150 nm时，从传感器表面传播的剪切波的反射和叠加现象变得更加清晰，同时位移增加（图3A和3C）。由于柔性膜的阻尼作用，与刚性薄膜相比，传感器表面上的位移要小得多。
当薄膜厚度增加到300 nm，阻尼效果会更加明显（图3A和3C）。由于振幅最初减小而后增大（波的相长/相消叠加），发射和反射剪切波之间的叠加产生的影响也更加明显。
在1微米厚的薄膜中（图3A），可以清楚地观察到振荡幅度的下降，以及在末端由于反射剪切波引起的振幅小幅上升。
对于5微米厚的薄膜，剪切波在到达上界面之前已完全消失，不会发生反射，因此不会出现叠加现象（3A）。
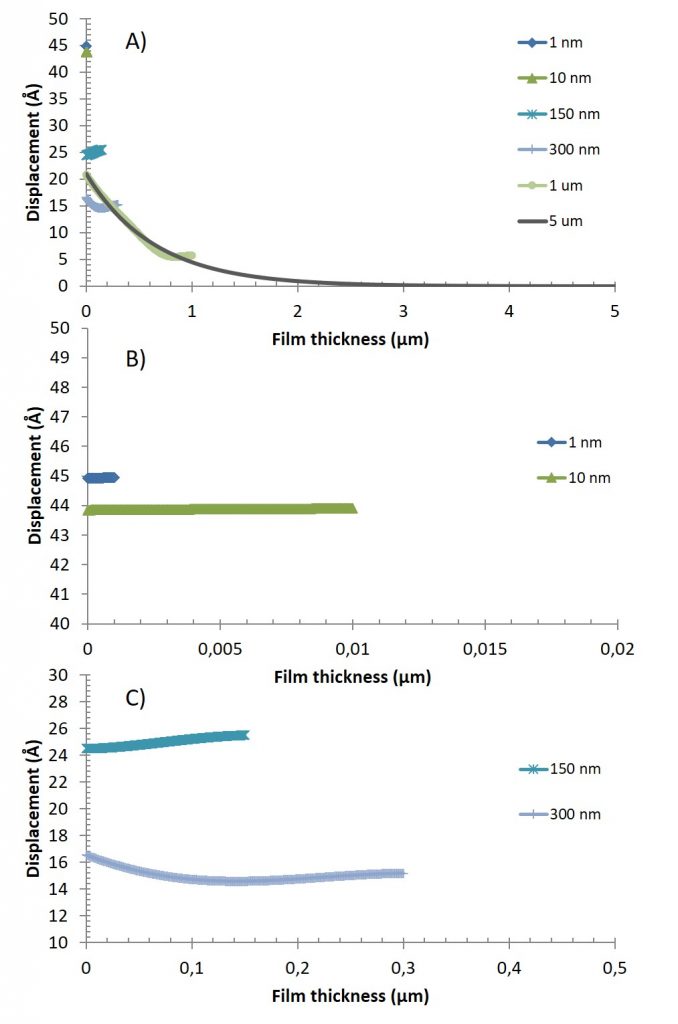
图3. 对应于1 nm、10 nm、150 nm、300 nm、1μm和5μm不同厚度薄膜，基频的剪切波振荡振幅变化。图A) 所有厚度的薄膜。图B）图A的局部放大图，突出显示1nm和10nm薄膜的行为。图C）图A的局部放大图，突出显示150nm和300nm薄膜的行为。
正如前面提到的，位移和消光深度随着倍频数的增加而变小(参见图2)。然而，其基本表现和与图3中基频观察到的结果一致。
倍频的f和D响应取决于薄膜性质
较低的共振可以感知较大的耦合质量，因此在横向均质膜的情况下，Δf和ΔD的相应响应通常较大（图4）。
如上所述，声波穿透深度δ和波长均随频率增加而减小。 因此，在较低的膜厚下，随着倍频数的增加，叠加效应将发生偏移，同时频率和能量耗散（最大反相位）的峰值将更早出现。
对于刚性膜，如本例中的Δf和ΔD较低，粘弹性响应不显著，因此所有倍频的f和D曲线发生重叠（图4）。 而当膜的柔性或本例中的薄膜厚度增加，在这种情况下，则会因穿透深度和波长的不同而产生明显的倍频分离。
随着薄膜厚度增加到δ以上，Δf和ΔD响应最终稳定在恒定值，此后不会感知到任何添加的物质，因此不会影响Δf和ΔD。
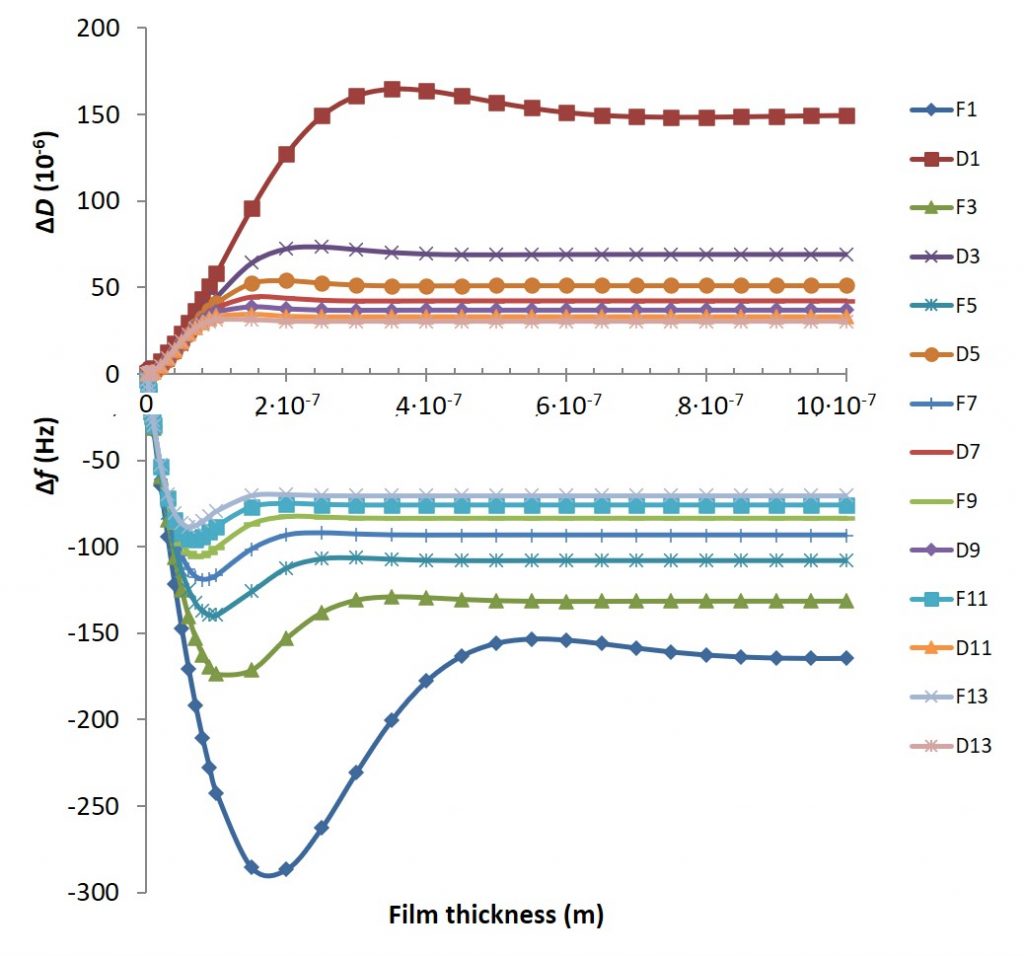图4.Δf和ΔD对不同倍频的响应随膜厚的变化。对于刚性薄膜，所有的倍频重叠，表明粘弹性响应不显著。随薄膜厚度的增加，倍频出现分离。
D/f的关系图说明了粘弹性响应的差异
对于不同的倍频，采用能量耗散ΔD对频率Δf作图时，粘弹性响应的差异变得更加明显（图5）。由于剪切波在柔性膜中的反射和叠加所产生的螺旋特性，导致一个特定的ΔD值可以对应两个、三个甚至四个不同的Δf值。
在螺旋图中，柔性膜质量负载的增加可能会导致Δf的增加，而在刚性膜时Δf通常会减小。柔性膜的表征不仅在于其质量或厚度，还在于其粘度和弹性模量。因此，仅使用一个倍频（即两个输入参数Δf和ΔD）将无法提供足够的信息来表征体系的粘弹性。对于不同的倍频，通过不同的Δf和ΔD值对构成的螺旋进行表征，由此提供的补充信息，可用于充分了解体系的行为。
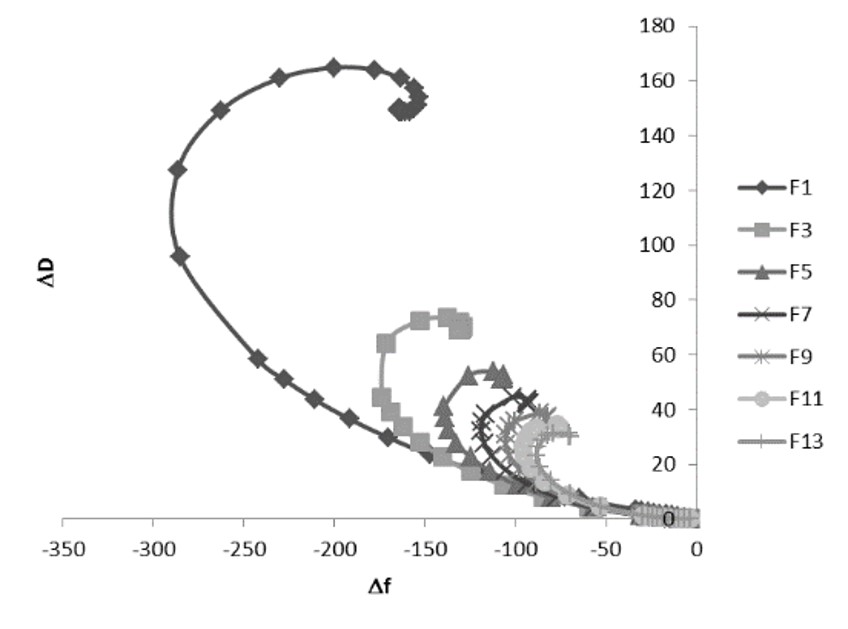图5. 对于不同的倍频，能量耗散ΔD与频率Δf变化的函数关系图。以这种方式作图，可以看到，一个特定的ΔD值可以对应于两个、三个甚至四个不同的Δf值。
结语
对于不同的倍频，同Δf和ΔD响应一样，振幅和叠加效应看起来也是不同的。 这再次让我们回到图1中所展示的结果，即倍频为研究与传感器表面接触的样品提供了不同的视角。
另外，弹性模型的数学模拟要求输入的参数数量不少于输出参数。对于一个柔性吸附层，输出的参数为质量/厚度、粘度和弹性。
如您想保存此文本以备后用，可下载PDF文件为什么QCM测量需要使用多个倍频？。
参考文献
24小时热线:400-833-6968
百欧林官方微信
